Random Forest From Top To Bottom

In three months (as of June 2016) the New Orleans Saints will play a football game against the Atlanta Falcons. I want to know who will win. I ask my friend and he says the Saints. Technically this is a predictive model, but it’s probably not worth much. I can improve upon this model by asking other people who they think will win. Someone might pick the Saints because we have a better quarterback. Someone else might pick the Saints because the game is at home. Another person might pick the Falcons to win because they’re a Falcons fan.

The point is that you can create a strong predictor from aggregating a bunch of weak (but better than random) predictors if they are uncorrelated. Combining my aunt’s prediction with my uncle’s prediction probably isn’t much better than using my aunt’s prediction alone because they use the same logic but when I include other people’s predictions which are based on things like “Who’s the home team?”, “Who won more games recently?”, “Who has the better defense?”, etc. the overall prediction should be much better than any of the individual predictions. This is the fundamental idea behind the random forest model. Now let’s use an example to see the gritty details behind bringing this idea to life.

Before you go further
Do you know what a decision/regression tree is and how it’s constructed? If I gave you a dataset could you construct one by hand? If not, read this article on decision trees and then come back.

Motivating Example

We want to predict whether the Saints will win a football game vs an opponent. Our training dataset consists of (fictitious) historical matches between the Saints and miscellaneous opponents. We’ve tracked some features we think might be important including

• the opponent’s overall rank at the time of the game
• whether or not the Saints were the home team
• predictions from a pair of so-called “experts”

Our target is simply a boolean feature indicating whether or not the Saints won.

You can find this data and some code from the Predict NFL Game Winner directory of the Machine Learning Problem Bible.

Opponent	OppRk	SaintsAtHome	Expert1PredWin	Expert2PredWin	SaintsWon
Falcons	28	TRUE	TRUE	TRUE	TRUE
Cowgirls	16	TRUE	TRUE	TRUE	TRUE
Eagles	30	FALSE	FALSE	TRUE	TRUE
Bucs	6	TRUE	FALSE	TRUE	FALSE
Bucs	14	TRUE	FALSE	FALSE	FALSE
Panthers	9	FALSE	TRUE	TRUE	FALSE
Panthers	18	FALSE	FALSE	FALSE	FALSE

Now consider what would happen if we grew a decision tree from this training data. Our decision tree would consist of a single split based on the Opponent feature. It just so happens that the Saints lost to the Bucs both times they played and the Saints lost to the Panthers both times they played. And since the Saints only played each of the other teams once, a decision tree will recognize that it can produce the following split Opponent in {Cowgirls, Eagles, Falcons} which will perfectly separate the target variable.

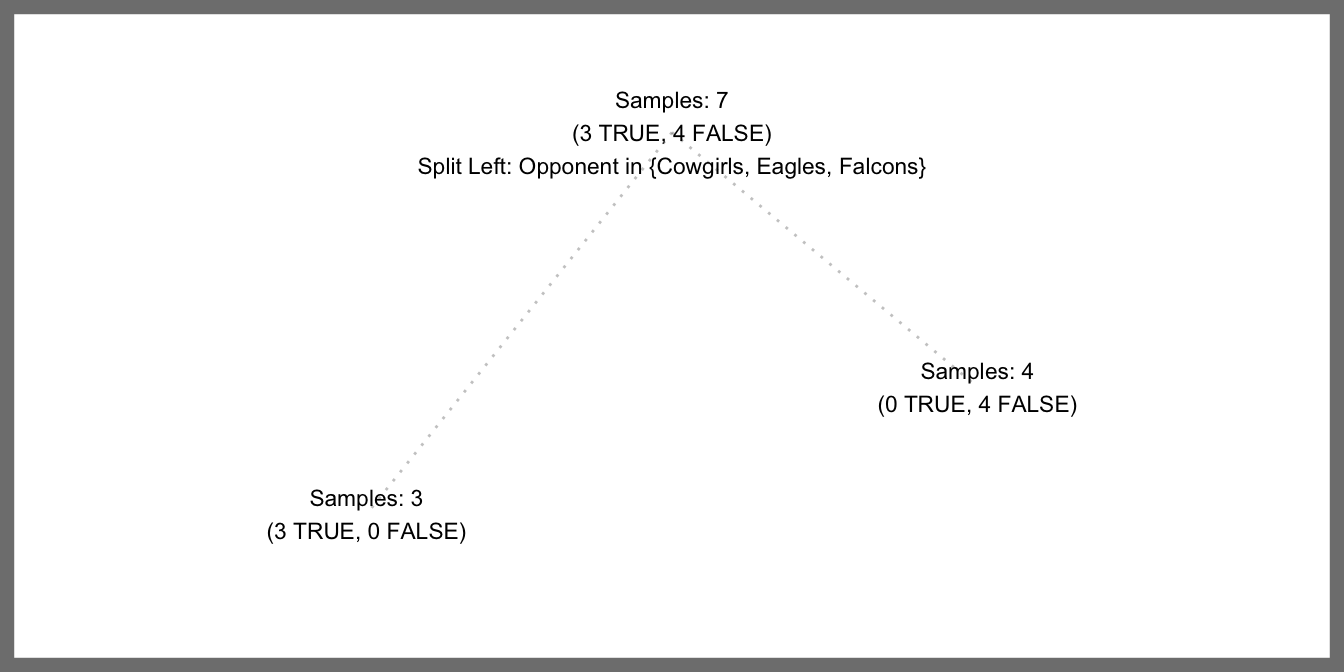
Our decision tree model is basically saying, “Hey, if you want to know whether you’re going to beat a team in the future just check whether you beat them in the past”. (Ignore the added complication that we might play a brand new team.) While there’s probably some merit to this, it’s still missing a lot of information that could help predict a winner. For example, Expert1 and Expert2 were each correct 71% of the time, so we’d like to include their input to some degree.

Big Idea 1

At each step in growing our decision tree, randomly select a subset of the features to try splitting the data (instead of trying every feature).

With this modified procedure, we can grow multiple, different decision trees. Then for a new sample we can let them vote on whether or not the Saints will win. In other words, we’ll build multiple weak but different classifiers which, together, should produce a really smart classifier. If we randomly choose three features to try at each split we could generate a forest with three decisions trees which might end up looking like this.

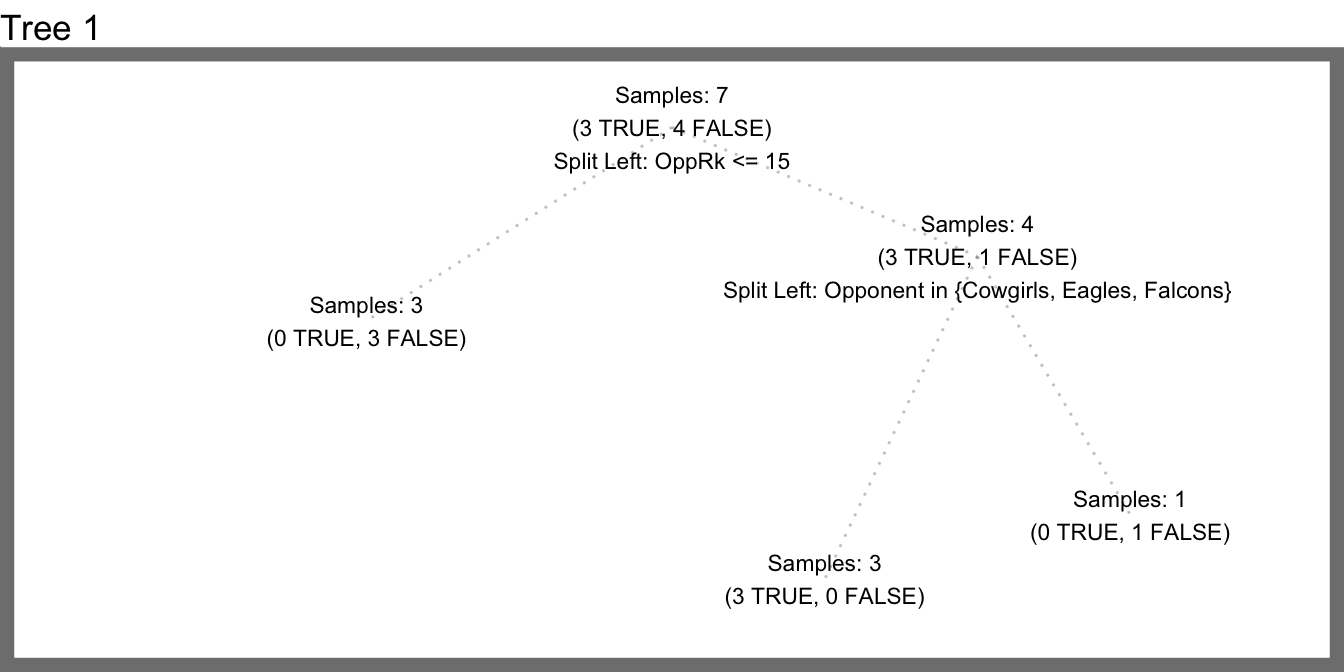
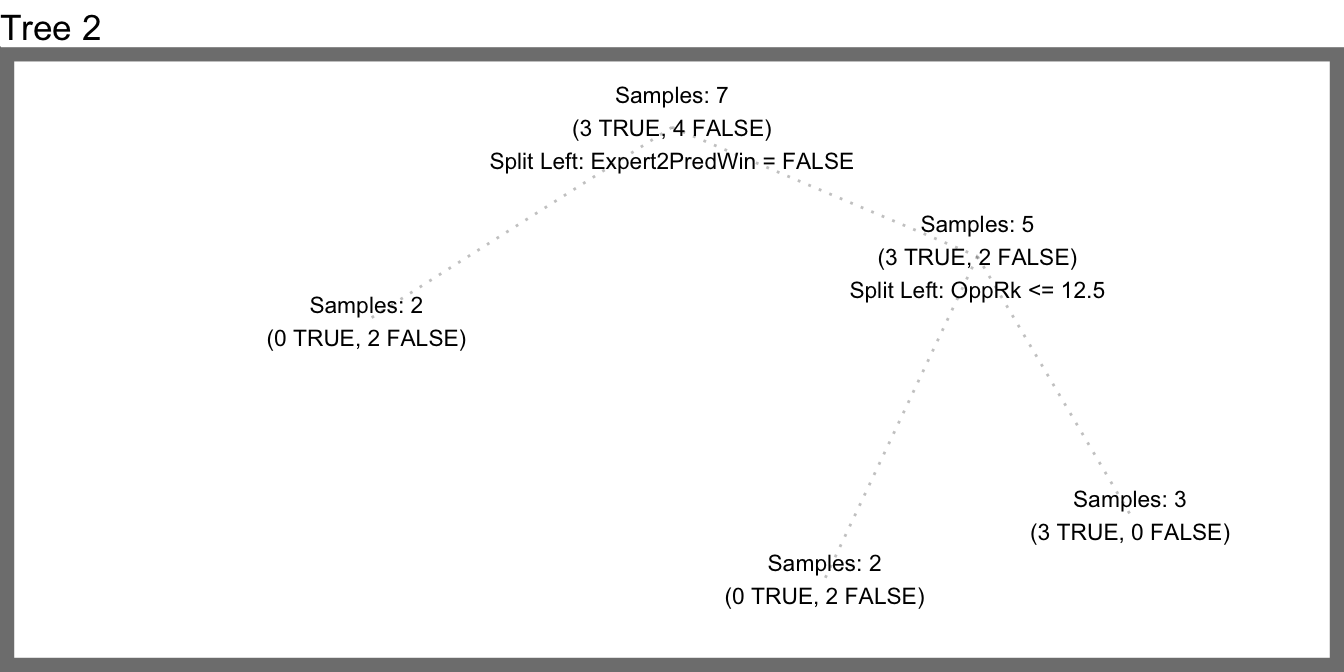
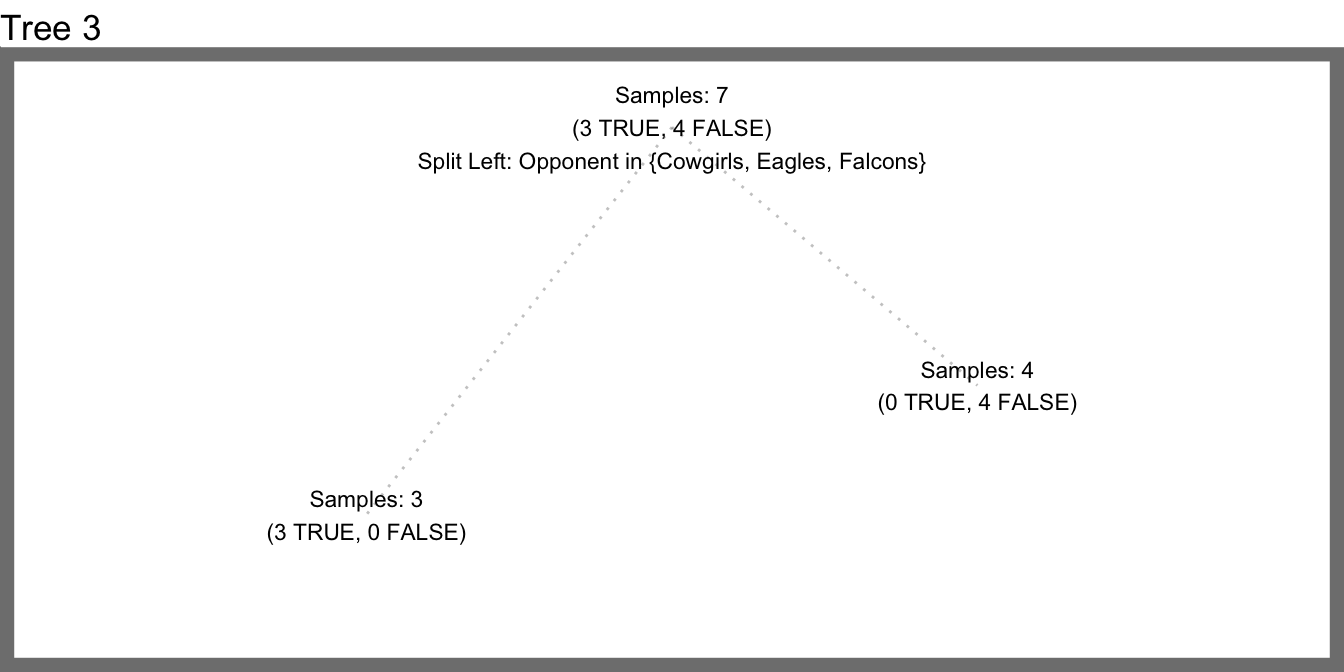
Let’s consider how this would perform on some hypothetical test data

Test Data

Opponent	OppRk	SaintsAtHome	Expert1PredWin	Expert2PredWin
Falcons	1	TRUE	TRUE	TRUE
Falcons	32	TRUE	TRUE	FALSE
Falcons	32	TRUE	FALSE	TRUE

Predictions

Sample	Tree1	Tree2	Tree3	MajorityVote
Sample1	TRUE	TRUE	TRUE	TRUE
Sample2	TRUE	TRUE	TRUE	TRUE
Sample3	TRUE	TRUE	TRUE	TRUE

With our random forest model we can even assign a probability/strength to each class (in this case {prob(TRUE), prob(FALSE)}) per sample by counting the number of trees who voted for that class divided by the total number of trees. Depending on the nature of the data, this might produce poor probability estimates but it will generally do a good job of ranking the likelihood of different classes.

Awesome. But we still have an issue. Consider the root node. Whenever Opponent gets selected as one of the three random features to attempt a split on, it will always win because it perfectly splits the target variable. However, the next best split (OppRk <= 15) is one sample away from being a perfect split. Yet, OppRk will become the root’s splitting feature only when Opponent is not randomly chosen as one of three initial features to try and OppRk is randomly chosen as one of three initial features to try. This means Opponent will become the root splitting feature 60% of the time whereas OppRk will become the root splitting feature just 30% of the time.

We can mitigate this issue by randomly selecting just two features to try at each split, but this could have unintended consequences. For example, if most of our features were poor predictors we’d end up producing a bunch of meaningless splits. On the other hand, we can randomly sample rows of the training data. If we randomly sample four of seven rows before growing a tree, almost half of the time OppRk will produce a perfect split and in these instances OppRk will be just as likely to be chosen as Opponent to be the root splitting feature.

Another point – suppose we sampled four features at each step. Then the feature SaintsAtHome could never split the root node because it would always be beaten by either Opponent or OppRk. But by sampling four rows before building each tree, SaintsAtHome could (albeit rarely) be chosen as the root splitting feature. The main point here is that sampling the training rows before growing each tree helps to generate uncorrelated decision trees which, when voting together, create a more powerful prediction than a set of very correlated trees. Also recognize that building decisions trees from random samples of our training data does not generate a biased model unless our sampling happens to be unlucky (which is easily fixed by growing more decision trees).

Big Idea 2-A

Before building each tree, randomly sample the rows of the training data.

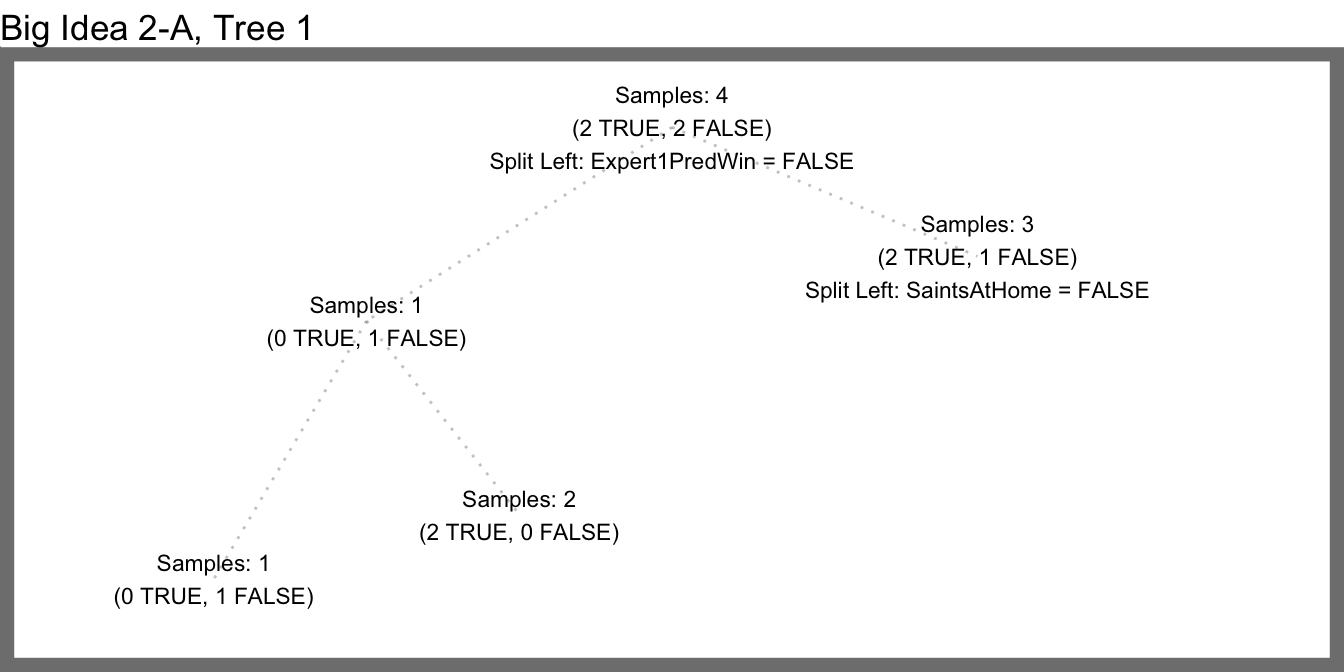
Continuing with our example, here we randomly select 4 of the 7 training samples before building each tree (while still trying three random features at each split).

2A - Samples 1

Opponent	OppRk	SaintsAtHome	Expert1PredWin	Expert2PredWin	SaintsWon
Cowgirls	16	TRUE	TRUE	TRUE	TRUE
Eagles	30	FALSE	FALSE	TRUE	TRUE
Panthers	9	FALSE	TRUE	TRUE	FALSE
Panthers	18	FALSE	FALSE	FALSE	FALSE

2A - Samples 2

Opponent	OppRk	SaintsAtHome	Expert1PredWin	Expert2PredWin	SaintsWon
Falcons	28	TRUE	TRUE	TRUE	TRUE
Cowgirls	16	TRUE	TRUE	TRUE	TRUE
Panthers	9	FALSE	TRUE	TRUE	FALSE
Panthers	18	FALSE	FALSE	FALSE	FALSE

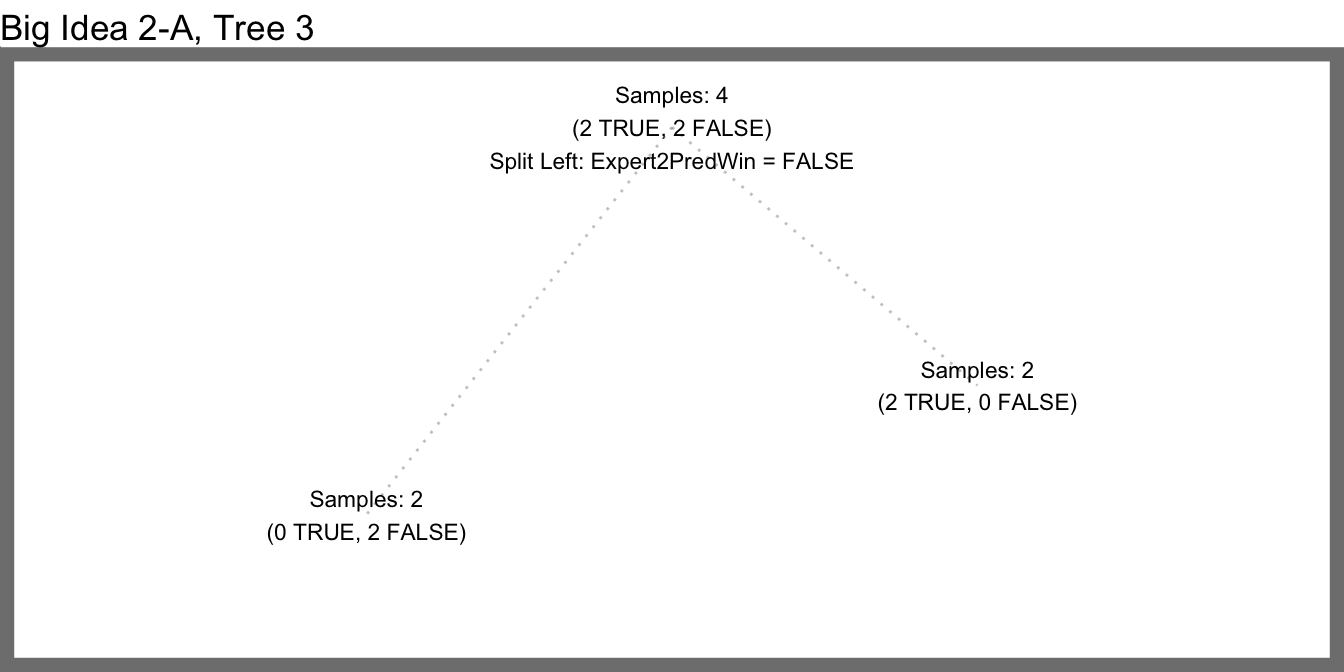
2A - Samples 3

Opponent	OppRk	SaintsAtHome	Expert1PredWin	Expert2PredWin	SaintsWon
Cowgirls	16	TRUE	TRUE	TRUE	TRUE
Eagles	30	FALSE	FALSE	TRUE	TRUE
Bucs	14	TRUE	FALSE	FALSE	FALSE
Panthers	18	FALSE	FALSE	FALSE	FALSE

Sweet. But we can still do better… Suppose Expert2 is a big Saints fan and part of his bias for the Saints factors into his predictions. Whenever he predicts the Saints to win, it doesn’t mean much but when he predicts the Saints to lose he’s always correct. Even though this fact is evident in the training data, our random forest model doesn’t do a good job of recognizing it. Wherever a tree splits based on SaintsAtHome, or OppRk <= 15, Expert2’s FALSE predictions get separated into different child nodes, so the information that Expert2 is always correct when he predicts the Saints to lose gets lost. This is fixed by sampling the training rows with replacement. And, since we’re sampling with replacement we can select a full 7 random rows before growing each tree without re-introducing the problems we discussed in the section above.

Big Idea 2-B

Before building each tree, randomly sample the rows of the training data with replacement.

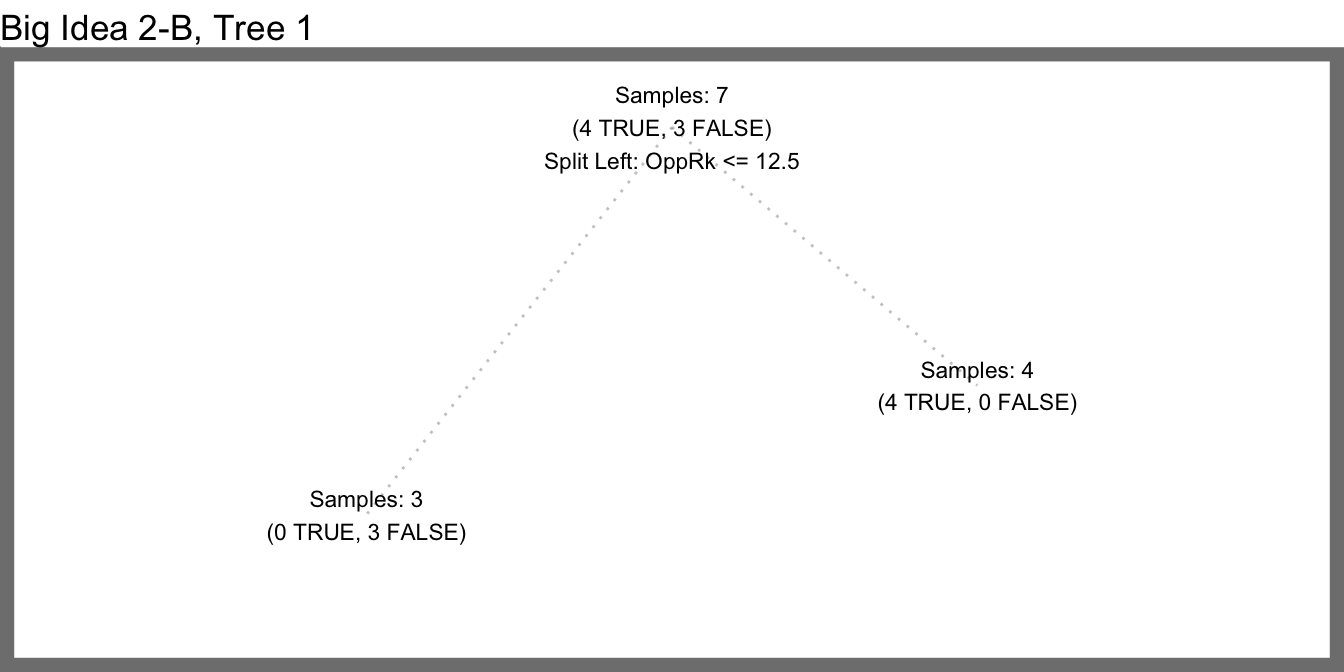
Here’s the next iteration in our random forest example where we choose 7 random rows with replacement before growing each tree (while still trying three random features at each split).

2B - Samples 1

Opponent	OppRk	SaintsAtHome	Expert1PredWin	Expert2PredWin	SaintsWon
Falcons	28	TRUE	TRUE	TRUE	TRUE
Cowgirls	16	TRUE	TRUE	TRUE	TRUE
Eagles	30	FALSE	FALSE	TRUE	TRUE
Eagles	30	FALSE	FALSE	TRUE	TRUE
Bucs	6	TRUE	FALSE	TRUE	FALSE
Panthers	9	FALSE	TRUE	TRUE	FALSE
Panthers	9	FALSE	TRUE	TRUE	FALSE

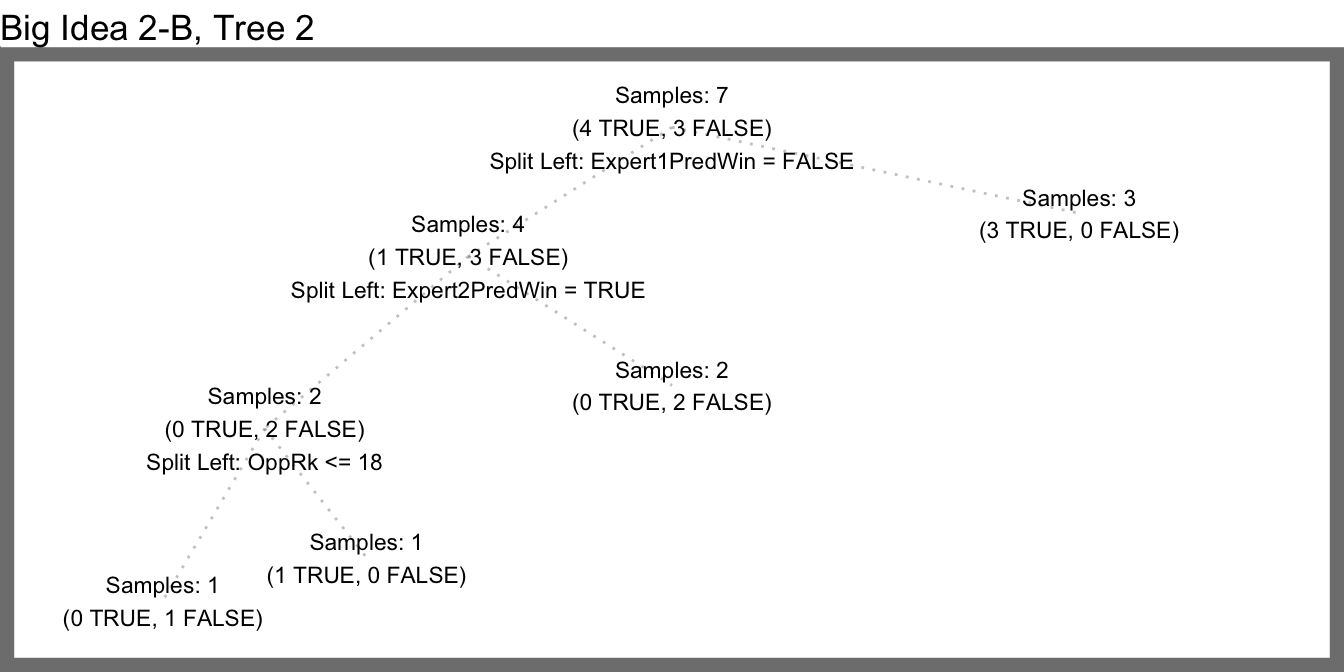
2B - Samples 2

Opponent	OppRk	SaintsAtHome	Expert1PredWin	Expert2PredWin	SaintsWon
Falcons	28	TRUE	TRUE	TRUE	TRUE
Falcons	28	TRUE	TRUE	TRUE	TRUE
Cowgirls	16	TRUE	TRUE	TRUE	TRUE
Eagles	30	FALSE	FALSE	TRUE	TRUE
Bucs	6	TRUE	FALSE	TRUE	FALSE
Bucs	14	TRUE	FALSE	FALSE	FALSE
Panthers	18	FALSE	FALSE	FALSE	FALSE

2B - Samples 3

Opponent	OppRk	SaintsAtHome	Expert1PredWin	Expert2PredWin	SaintsWon
Eagles	30	FALSE	FALSE	TRUE	TRUE
Bucs	14	TRUE	FALSE	FALSE	FALSE
Bucs	14	TRUE	FALSE	FALSE	FALSE
Panthers	9	FALSE	TRUE	TRUE	FALSE
Panthers	9	FALSE	TRUE	TRUE	FALSE
Panthers	18	FALSE	FALSE	FALSE	FALSE
Panthers	18	FALSE	FALSE	FALSE	FALSE

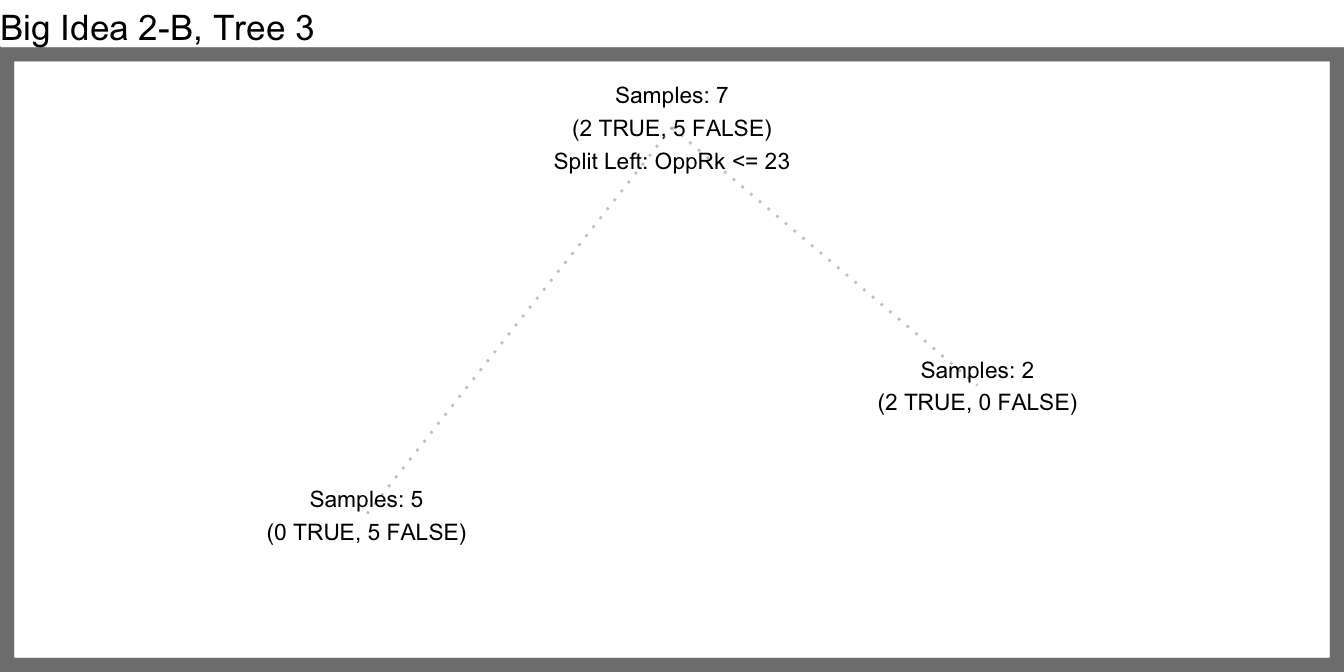
Predictions

Sample	Tree1	Tree2	Tree3	MajorityVote
Sample1	FALSE	TRUE	FALSE	FALSE
Sample2	TRUE	TRUE	TRUE	TRUE
Sample3	TRUE	TRUE	TRUE	TRUE

Recapping

Our random forest model is best described as an algorithm:

1. Determine how many trees, B, to grow (in our example B = 3)
2. For each tree
   1. Randomly sample N rows of the training data with replacement (in our example N = 7)
   2. Grow a decision tree such that the best of m random features is used to split the data at each non-leaf node (in our example m = 3)
3. For a new sample combine the predictions from the trees, either by majority vote (for classification) or averaging (for regression).

Cleaning Up Loose Ends

If your mind isn’t blown you probably have some lingering questions. I’ll do my best to answer them here.

Huh? The way you described the Opponent feature and how it gets split isn’t what I’m used to from Python and Scikit-Learn

Yup. This is due to a deficiency in Scikit-Learn which requires categorical features to be one-hot encoded. (In our example Opponent would need to be replaced with five features: {OppBucs, OppCowgirls, …} each with TRUE/FALSE values.) This is a deficiency and it’s currently being addressed by the Scikit-Learn development team.

Suppose the Saints play a new team – one not seen in the training data. How would random forest make a prediction for it?

The answer to this really regards the behavior of a decision tree. (In fact, most questions/confusion about random forest can be answered by reviewing the details of constructing a decision tree.) R’s randomForest package (used to generate the examples in this article) currently always sends new categories down the right branch in each split on said category. I spoke with Andy Liaw (the package’s maintainer) who agrees this behavior is sub-optimal (as of version 4.6-12) but we haven’t agreed on the best solution. If you use Scikit-Learn you would be forced to one-hot encode categorical features, in which case this problem won’t be a problem.

How many trees should I build? How many rows should I sample before growing each tree? How deep should each tree be?

On other words, “How do I tune the hyperparameters of a random forest?” This question isn’t specific to random forest. The most common approach is to use grid-search + cross validation – essentially “guess and check” where the training phase is based on one dataset and the testing phase is based on another. Otherwise, here are some notes specific to random forest:

• The more trees the better. But at a certain point the next tree just slows down your computer without adding more predictive power
• Leo Breiman (random forest’s creator) suggests sampling (with replacement) n rows from the training set before growing each tree where n = number of rows in the training set. This technique is known as bagging and will result in roughly 63% of the unique training samples being used to construct a single decision tree.

Props to Leo Breiman for developing this awesome algorithm. (Although, these days it’s frequently outperformed by gradient boosting.) For more details, check out Breiman’s own writeup on random forest.