Making A Binary Search Tree in C++
This article is about implementing a Binary Search Tree (BST) in C++. I’ll skip the part about defining what a BST is since that’s a horse that’s been beaten many times. I am new to C++, so my implementation may have flaws. I welcome and encourage critique from other programmers :)
Draft 1
We start by implementing a TreeNode struct.
struct TreeNode
{
// member vars
int data;
TreeNode* left;
TreeNode* right;
// constructor
TreeNode(int data): data(data), left(nullptr), right(nullptr) {}
};
Notes:
- Each TreeNode has three member variables:
- data, an int storing the node’s value. In the future we can use template programming so that data can be any comparable type.
- left a pointer to the left child node which is also a TreeNode
- right a pointer to the left child node which is also a TreeNode
- Our constructor lets us build a new TreeNode by providing a single int value, and it sets left and right to nullptrs.
Let’s play with it. We’ll start by making a single node with the value 5.
#include <iostream>
struct TreeNode
{
// member vars
int data;
TreeNode* left;
TreeNode* right;
// constructor
TreeNode(int data): data(data), left(nullptr), right(nullptr) {}
};
int main() {
// Make a new TreeNode
TreeNode foo(5);
// Print info about foo
std::cout <<
"data: " << foo.data <<
", left: " << foo.left <<
", right: " << foo.right <<
std::endl;
return 0;
}
Challenge
Build a binary tree with 5 as the root node connected to 4 (left child) and 6 (right child).
Solution
#include <iostream>
// struct TreeNode{...}
int main() {
// Make the tree
// 5
// / \
// 4 6
// Make the nodes
TreeNode root(5);
TreeNode leftChild(4);
TreeNode rightChild(6);
// Connect nodes
root.left = &leftChild;
root.right = &rightChild;
// Print info about the root
std::cout <<
"data: " << root.data <<
", left: " << root.left->data <<
", right: " << root.right->data <<
std::endl;
return 0;
}
data: 5, left: 4, right: 6
Draft 2
Right now, we can’t initialize an empty BST from our model. In order to allow for empty trees, we’ll make a BSTree class that stores a pointer to the root TreeNode (which might be null). This class has the added benefit that it gives us a distinction of the tree as a whole and it’s nodes or subtrees.
#include <iostream>
// struct TreeNode{...}
class BSTree
{
public:
// constructors
BSTree(): root(nullptr) {}
BSTree(TreeNode* rootNode): root(rootNode) {}
// member functions
void Print();
private:
TreeNode* root;
};
Challenge
Implement the member function Print().
Solution
This method won’t print the prettiest trees, but it’ll be good enough to visualize the structure of small trees.
#include <iostream>
#include <string>
// struct TreeNode{...}
class BSTree
{
public:
// constructors
BSTree(): root(nullptr) {}
BSTree(TreeNode* rootNode): root(rootNode) {}
// member functions
void Print();
private:
TreeNode* root;
std::string SubTreeAsString(TreeNode* node); // Helper method for Print()
};
/// Print the tree
void BSTree::Print(){
if(this->root == nullptr){
std::cout << "{}" << std::endl;
} else{
std::cout << this->SubTreeAsString(this->root) << std::endl;
}
}
/// Print the subtree starting at '*node'
std::string BSTree::SubTreeAsString(TreeNode* node){
std::string leftStr = (node->left == nullptr) ? "{}" : SubTreeAsString(node->left);
std::string rightStr = (node->right == nullptr) ? "{}" : SubTreeAsString(node->right);
std::string result = "{" + std::to_string(node->data) + ", " + leftStr + ", " + rightStr + "}";
return result;
}
And some tests…
int main() {
// -----------------------------
// Make and print an empty tree
BSTree emptyTree {};
emptyTree.Print();
// -----------------------------
// Make and print the tree
// 5
// / \
// 4 6
// Make the nodes
TreeNode root(5);
TreeNode leftChild(4);
TreeNode rightChild(6);
// Connect nodes
root.left = &leftChild;
root.right = &rightChild;
// Make and print the tree
BSTree myTree {&root};
myTree.Print();
return 0;
}
{}
{5, {4, {}, {}}, {6, {}, {}}}
Notes:
- Here we represent each node as a set of three elements, {data, leftChild, rightChild} with empty trees represented as {}.
- We use a private helper method
SubTreeAsString(TreeNode* node)that recursively pieces together a string representation of the current node’s data and string representations of it’s children’s data.
Draft 3
Here we add an Insert(int val) method for inserting new nodes into the tree. With this method in place, we’ll be able to construct trees naturually by initializing an empty tree and then doing a series of inserts as opposed to what we’ve been doing - awkwardly making node instances and manually stitching them together. Note that if a user tries to add a value that already exists in the tree, we’ll warn them about it and then do nothing.
#include <iostream>
#include <string>
// struct TreeNode{...}
class BSTree
{
public:
// constructors
BSTree(): root(nullptr) {}
BSTree(TreeNode* rootNode): root(rootNode) {}
// member functions
void Print();
void Insert(int val);
private:
TreeNode* root;
std::string SubTreeAsString(TreeNode* node); // Helper method for Print()
void Insert(int val, TreeNode* node); // Helper method for Insert(int val)
};
/// Insert a new value into the tree
void BSTree::Insert(int val) {
if(root == nullptr){
this->root = new TreeNode(val);
} else{
this->Insert(val, this->root);
}
}
/// Insert a new value into the subtree starting at node
void BSTree::Insert(int val, TreeNode* node) {
// Check if node's value equals val
// If so, warn the user and then exit function
if(val == node->data){
std::cout << "Warning: Value already exists, so nothing will be done." << std::endl;
return;
}
// Check if val is < or > this node's value
if(val < node->data){
if(node->left == nullptr){
// Make a new node as the left child of this node
node->left = new TreeNode(val);
} else{
// Recursively call Insert() on this node's left child
this->Insert(val, node->left);
}
} else{
if(node->right == nullptr){
// Make a new node as the right child of this node
node->right = new TreeNode(val);
} else{
// Recursively call Insert() on this node's right child
this->Insert(val, node->right);
}
}
}
Notes:
- Here we use a public
Insert(int val)method for inserting a new node into the tree and a privateInsert(int val, TreeNode* node)helper method for inserting a new node into the subtree starting at the given node. Insert(int val)handles the special case of, when the tree is empty, making a new node that becomes the root.Insert(int val, TreeNode* node)handles the recursive logic, If val is less than the current node’s value, insert val into the subtree starting at the current node’s left child, otherwise insert it into the subtree starting at it’s right child. This method uses arm’s-length recursion whereby each call toInsert(int val, TreeNode* node)checks if the left/right child is null before recurively callingInsert(int val, TreeNode* node)on a pointer to that child node. If the child is null, then instead of making the recurvise call, we stop and make the new node right there and point the current node at it.
Let’s try it.
int main() {
BSTree myTree {};
myTree.Print();
myTree.Insert(5);
myTree.Print();
myTree.Insert(4);
myTree.Print();
myTree.Insert(6);
myTree.Print();
return 0;
}
{} {5, {}, {}} {5, {4, {}, {}}, {}} {5, {4, {}, {}}, {6, {}, {}}}
Indeed our Insert(int val) works! But there’s a nagging issue..
Draft 4
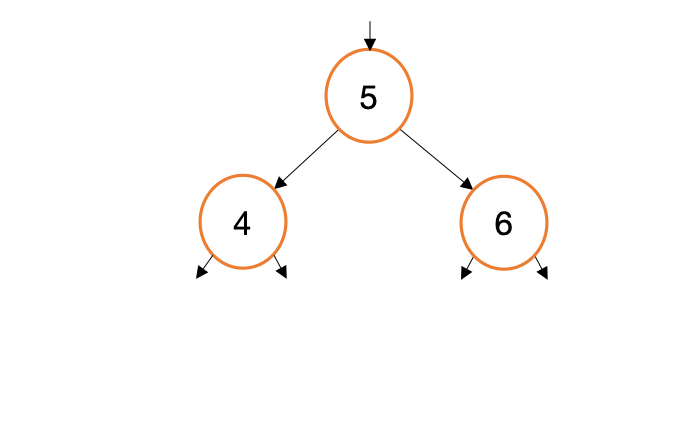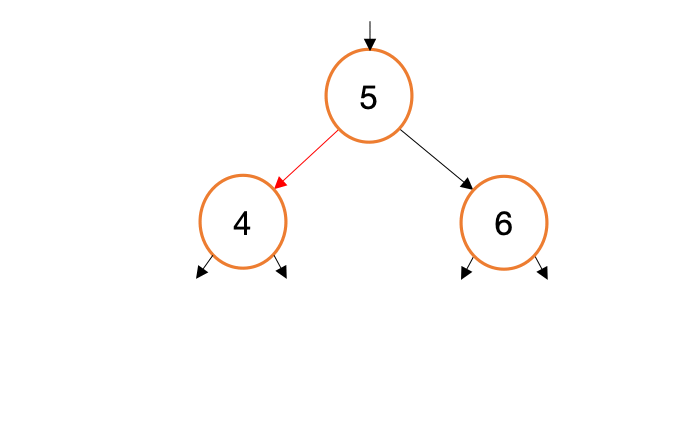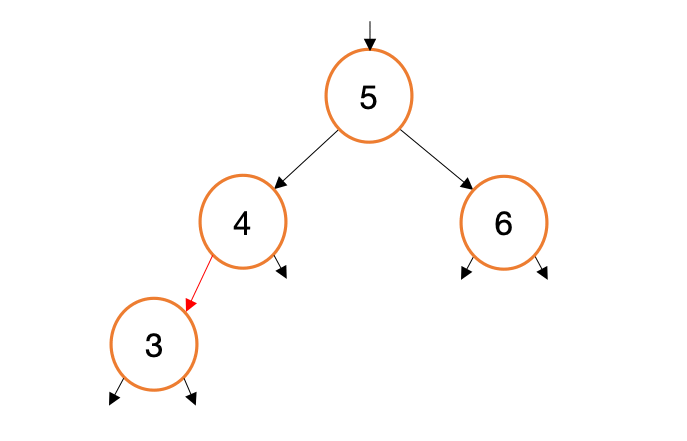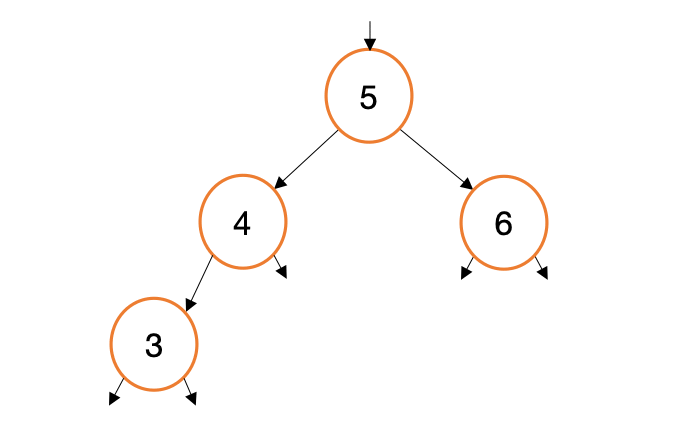
Suppose we want to add a new value, 3, to the tree we just created. Let’s visualize how this process will work..
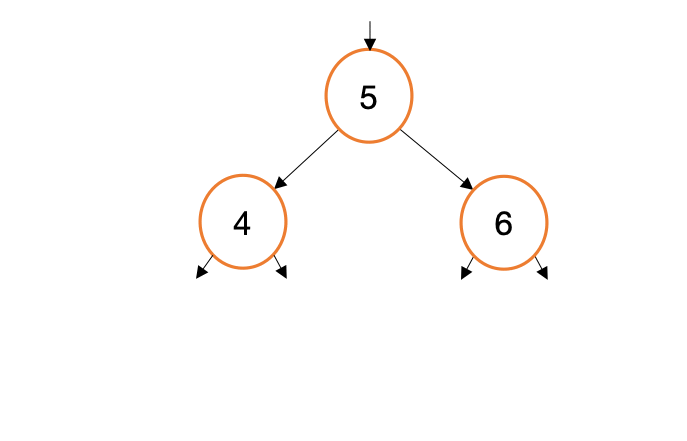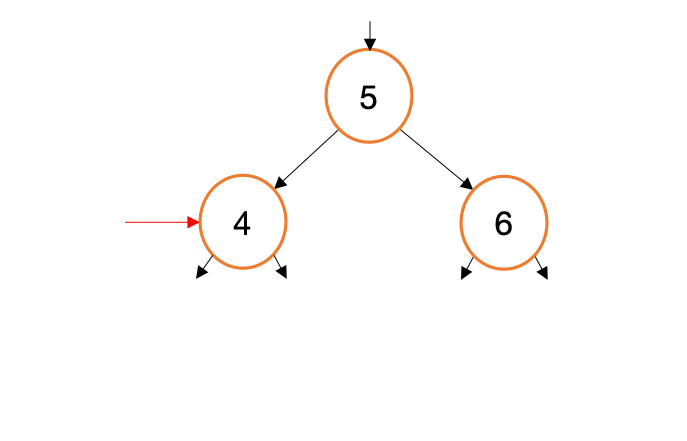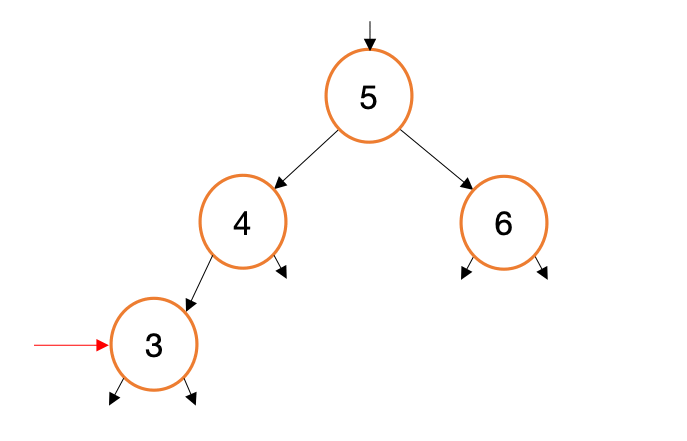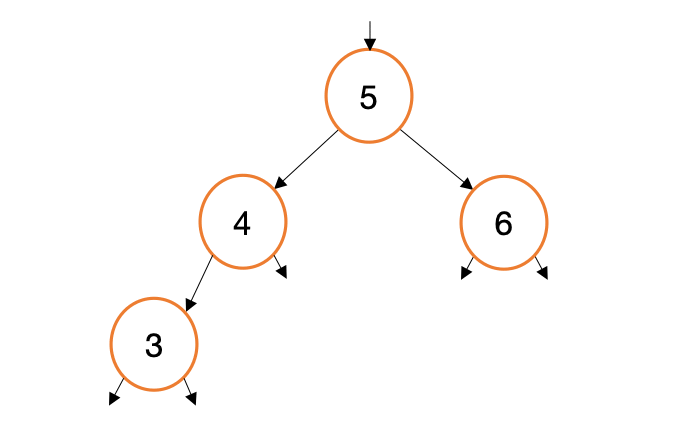
When we call myTree.Insert(3) this generates three calls to Insert(int val, TreeNode* node). For each of these calls, we are generating copies of a node pointer (new, red arrows in the gif above). This begs the question, Why not traverse the existing node pointers instead of making copies? Indeed, such a design would be simpler and more efficient.
The trick to making this work is that we need to change Insert(int val, TreeNode* node) to Insert(int val, TreeNode*& node), passing each node pointer as a reference instead of a copy. With this this modification in place, it simplifies the logic for both Insert(int val) and Insert(int val, TreeNode*& node) because it lets us recursively traverse the tree until we reach a nullptr and then insert a new node as opposed to our previous arm’s length recursion technique.
#include <iostream>
#include <string>
// struct TreeNode {...}
class BSTree
{
public:
// constructors
BSTree(): root(nullptr) {}
BSTree(TreeNode* rootNode): root(rootNode) {}
// member functions
void Print();
void Insert(int val);
private:
TreeNode* root;
std::string SubTreeAsString(TreeNode* node); // Helper method for Print()
void Insert(int val, TreeNode*& node); // Helper method for Insert(int val)
};
/// Insert a new value into the tree
void BSTree::Insert(int val) {
this->Insert(val, this->root);
}
/// Insert a new value into the subtree starting at node
void BSTree::Insert(int val, TreeNode*& node) {
if(node == nullptr){
// Case: node is a nullptr
// Make a new TreeNode for it to point to
node = new TreeNode(val);
} else{
if(val < node->data){
// Case: val is < node's data
this->Insert(val, node->left);
} else if(val > node->data){
// Case: val is > node's data
this->Insert(val, node->right);
} else{
// Case: val is equal to node's data
std::cout << "Warning: Value already exists, so nothing will be done." << std::endl;
}
}
}
Draft 5
One use case for a BST is a dynamic set. For example, we could use a BST to create a dictionary of the unique words in a book. At the end of this process, we might want to check if a certain word is in the dictionary (and therefore in the book). Along these lines, let’s implement a Contains(int val) method that checks if a value exists in our BSTree.
#include <iostream>
#include <string>
// struct TreeNode {...}
class BSTree
{
public:
// constructors
BSTree(): root(nullptr) {}
BSTree(TreeNode* rootNode): root(rootNode) {}
// member functions
void Print();
void Insert(int val);
bool Contains(int val);
private:
TreeNode* root;
std::string SubTreeAsString(TreeNode* node); // Helper method for Print()
void Insert(int val, TreeNode*& node); // Helper method for Insert(int val)
bool Contains(int val, TreeNode*& node); // Helper method for Contains(int val)
};
/// Check if the given value exists in the BSTree
bool BSTree::Contains(int val) {
return Contains(val, this->root);
}
/// Check if the given value exists in the subtree
/// starting at node
bool BSTree::Contains(int val, TreeNode*& node) {
if(node == nullptr){
return false;
} else if(val == node->data){
return true;
} else if(val < node->data){
return this->Contains(val, node->left);
} else{
return this->Contains(val, node->right);
}
}
Now let’s test it.
int main() {
BSTree myTree {};
myTree.Insert(5);
myTree.Insert(4);
myTree.Insert(6);
std::cout << std::boolalpha << myTree.Contains(4) << std::endl;
std::cout << std::boolalpha <<myTree.Contains(2) << std::endl;
return 0;
}
true false
Looks good.
Draft 6
Now lets implement Remove(int val) for removing a single node from a tree. In determinig the logic for removing a node, we need to consider five cases.
-
val doesn’t exist
We notify the user and then do nothing. -
val exists at a leaf node
We delete the node. -
val exists at a node with a left child but not a right child
We make the node’s parent point at the node’s left child and then delete the node. -
val exists at a node with a right child but not a left child
We make the node’s parent point at the node’s right child and then delete the node. -
val exists at a node with left and right children
This is the tricky case, but the solution is elegantly simple. We replace the node’s value with the minimum value in its right subtree. Then we delete that node (i.e the min-value node from the right subtree we just found). Convince yourself that the resulting tree is still a valid Binary Search Tree. (Note that there are other solutions to this problem.)
#include <iostream>
#include <string>
// struct TreeNode{...}
class BSTree
{
public:
// constructors
BSTree(): root(nullptr) {}
BSTree(TreeNode* rootNode): root(rootNode) {}
// member functions
void Print();
void Insert(int val);
bool Contains(int val);
void Remove(int val);
private:
TreeNode* root;
std::string SubTreeAsString(TreeNode* node); // Helper method for Print()
void Insert(int val, TreeNode*& node); // Helper method for Insert(int val)
bool Contains(int val, TreeNode*& node); // Helper method for Contains(int val)
void Remove(int val, TreeNode*& node); // Helper method for Remove(int val)
TreeNode*& FindMin(TreeNode*& node); // Helper method for Remove(int val)
};
/// Remove given value from the tree
void BSTree::Remove(int val) {
this->Remove(val, this->root);
}
/// Remove given value from the subtree starting at node
void BSTree::Remove(int val, TreeNode*& node) {
if(node == nullptr){
// Case: nullptr
std::cout << "val not found in tree" << std::endl;
} else if(val == node->data){
// Found value
TreeNode* trash = nullptr;
if(node->left == nullptr && node->right == nullptr){
// Case: node is a leaf
trash = node;
node = nullptr;
} else if(node->left != nullptr && node->right == nullptr){
// Case: node has a left subtree (but not right)
// Point node's parent at node's left subtree
trash = node;
node = node->left;
} else if(node->left == nullptr && node->right != nullptr){
// Case: node has a right subtree (but not left)
trash = node;
node = node->right;
} else{
// Case: node has left and right subtrees
TreeNode*& minNode = this->FindMin(node->right); // returns a reference to the pointer in the tree
node->data = minNode->data;
this->Remove(minNode->data, minNode);
}
// Free memory
if(trash != nullptr) delete trash;
} else if(val < node->data){
// Case: remove val from this node's left subtree
this->Remove(val, node->left);
} else{
// Case: remove val from this node's right subtree
this->Remove(val, node->right);
}
}
/// Search the subtree starting at node and return a pointer to the minimum-value node
/// The returned pointer will be a reference of an actual pointer in the tree, not a copy
TreeNode*& BSTree::FindMin(TreeNode*& node) {
if(node == nullptr){
throw "Min value not found";
} else if(node->left == nullptr){
return node;
} else{
return this->FindMin(node->left);
}
}
Notes:
void BSTree::Remove(int val, TreeNode*& node)does the heavy liftingTreeNode*& BSTree::FindMin(TreeNode*& node)is a helper method that finds and returns a reference to the tree’s pointer that points at the smallest node in the subtree starting at the given node.- Whenever we delete a node, we make sure to delete the TreeNode object, freeing up memory on the heap
Draft 7
Finally, we’ll identify and implement a number of improvements, giving our rough implementation a more polished feel.
- Currently we’re using raw pointers, but it’d be better to replace those raw pointer with smart pointers so that we don’t need to worry about memory leaks and we don’t have to manage the deletion of objects ourselves when we move nodes around.
- There’s really no reason to expose TreeNode to the user. It’d be better to declare TreeNode as a private member of our BSTree class.
- Right now our BSTree can only be comprised of ints. With template programming, we can let our users build a BSTree with any type that is comparable.
- Many of our mthods use but don’t modify their input/out. We should declare such variables as const.
Challenge
Implement those improvements.
Solution
#include <iostream>
#include <string>
#include <memory> // unique_ptr
template <typename T>
class BSTree
{
public:
// constructors
BSTree(): root(nullptr) {}
// member functions
void Print() const;
void Insert(T val);
bool Contains(T val) const;
void Remove(T val);
private:
struct TreeNode
{
// member vars
T data;
std::unique_ptr<TreeNode> left;
std::unique_ptr<TreeNode> right;
// constructor
TreeNode(T data): data(data), left(nullptr), right(nullptr) {}
};
std::unique_ptr<TreeNode> root;
std::string SubTreeAsString(const std::unique_ptr<TreeNode>& node) const; // Helper method for Print()
void Insert(T val, std::unique_ptr<TreeNode>& node); // Helper method for Insert(int val)
bool Contains(T val, std::unique_ptr<TreeNode>& node) const; // Helper method for Contains(int val)
void Remove(T val, std::unique_ptr<TreeNode>& node); // Helper method for Remove(int val)
std::unique_ptr<TreeNode>& FindMin(std::unique_ptr<TreeNode>& node); // Helper method for Remove(int val)
};
/// Print the tree
template <typename T>
void BSTree<T>::Print() const {
if(this->root == nullptr){
std::cout << "{}" << std::endl;
} else{
std::cout << this->SubTreeAsString(this->root) << std::endl;
}
}
/// Print the subtree starting at node
template <typename T>
std::string BSTree<T>::SubTreeAsString(const std::unique_ptr<TreeNode>& node) const {
std::string leftStr = (node->left == nullptr) ? "{}" : SubTreeAsString(node->left);
std::string rightStr = (node->right == nullptr) ? "{}" : SubTreeAsString(node->right);
std::string result = "{" + std::to_string(node->data) + ", " + leftStr + ", " + rightStr + "}";
return result;
}
/// Insert a new value into the tree
template <typename T>
void BSTree<T>::Insert(T val) {
this->Insert(val, this->root);
}
/// Insert a new value into the subtree starting at node
template <typename T>
void BSTree<T>::Insert(T val, std::unique_ptr<TreeNode>& node) {
if(node == nullptr){
// Case: node is a nullptr
// Make a new TreeNode for it to point to
node = std::make_unique<TreeNode>(val);
} else{
if(val < node->data){
// Case: val is < node's data
this->Insert(val, node->left);
} else if(val > node->data){
// Case: val is > node's data
this->Insert(val, node->right);
} else{
// Case: val is equal to node's data
std::cout << "Warning: Value already exists, so nothing will be done." << std::endl;
}
}
}
/// Check if the given value exists in the BSTree
template <typename T>
bool BSTree<T>::Contains(T val) const {
return Contains(val, this->root);
}
/// Check if the given value exists in the subtree
/// starting at node
template <typename T>
bool BSTree<T>::Contains(T val, std::unique_ptr<TreeNode>& node) const {
if(node == nullptr){
return false;
} else if(val == node->data){
return true;
} else if(val < node->data){
return this->Contains(val, node->left);
} else{
return this-Contains(val, node->right);
}
}
/// Remove given value from the tree
template <typename T>
void BSTree<T>::Remove(T val) {
this->Remove(val, this->root);
}
/// Remove given value from the subtree starting at node
template <typename T>
void BSTree<T>::Remove(T val, std::unique_ptr<TreeNode>& node) {
if(node == nullptr){
// Case: nullptr
std::cout << "val not found in tree" << std::endl;
} else if(val == node->data){
// Found value
if(node->left == nullptr && node->right == nullptr){
// Case: node is a leaf
node = nullptr;
} else if(node->left != nullptr && node->right == nullptr){
// Case: node has a left subtree (but not right)
// Point node's parent at node's left subtree
node = std::move(node->left);
} else if(node->left == nullptr && node->right != nullptr){
// Case: node has a right subtree (but not left)
node = std::move(node->right);
} else{
// Case: node has left and right subtrees
std::unique_ptr<TreeNode>& minNode = this->FindMin(node->right); // returns a reference to the actual pointer in the tree
node->data = minNode->data;
this->Remove(minNode->data, minNode);
}
} else if(val < node->data){
// Case: remove val from this node's left subtree
this->Remove(val, node->left);
} else{
// Case: remove val from this node's right subtree
this->Remove(val, node->right);
}
}
/// Search the subtree starting at node and return a pointer to the minimum-value node
/// The returned pointer will be a reference of an actual pointer in the tree, not a copy
template <typename T>
std::unique_ptr<typename BSTree<T>::TreeNode>& BSTree<T>::FindMin(std::unique_ptr<TreeNode>& node) {
if(node == nullptr){
throw "Min value not found";
} else if(node->left == nullptr){
return node;
} else{
return this->FindMin(node->left);
}
}
Special thanks to Marty Stepp and his fantastic Stanford lectures on implementing Binary Search Trees in C++.
 GormAnalysis
GormAnalysis